Sách kỹ sư/Điện từ
Điện từ một hiện tượng tìm thấy trong tương tác giửa dẩn điện và điện có dòng điện khác không tạo ra từ có từ trường giống như từ trường của Nam châm thường ; một vật có khả năng hút kim loại nằm trong từ trường
Nam châm
sửaNam châm là một vật liệu hoặc vật thể tạo ra từ trường của các đường lực từ vô hình có khả năng hút mọi vật từ nằm kề bên nam châm
Tính chất nam châm
sửaMọi Nam châm đều có
- 2 cực , Cực bắc và Cực nam
- Từ trường tạo ra từ các đường sức lực (Lực từ) đi từ cực bắc đến cực nam
- Khả năng hút vật liệu từ như Sắt, Nam châm khác về hướng mình1
Loại Nam châm
sửaNam châm thường
sửaNam châm là một vật liệu hoặc vật thể tạo ra từ trường. Từ trường này vô hình và có khả năng tạo ra lực từ có khả năng hút các vật liệu sắt nằm kề bên nam châm
Nam châm điện thường
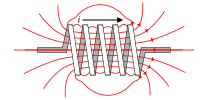
sửaThí nghiệm cho thấy, Nam châm điện thường được tạo ra từ mắc nối các dẩn điện như Cộng dây thẳng dẩn điện, Vòng tròn dẩn điện và Cuộn tròn dẩn điện với điện
Nam châm điện thường tạo ra từ các lối mắc trên đều có các tính chất sau
- Từ sinh khi Nam châm điện thường dẩn điện
- I ≠ 0 . B ≠ 0 = LI
- Từ biến mất khi Nam châm điện thường không dẩn điện
- I = 0 . B = 0
Với
Nam châm điện vĩnh cửu
sửaThí nghiệm cho thấy, Nam châm điện vĩnh cửu được tạo ra bằng cách để một từ vật nằm trong các vòng tròn của cuộn tròn dẩn điện mắc nối với điện
Nam châm điện vỉnh cửu tạo ra từ lối mắc trên có các tính chất sau
- Từ sinh khi Nam châm điện thường dẩn điện
- I ≠ 0 . B ≠ 0 . H ≠ 0
- Từ biến mất khi Nam châm điện thường không dẩn điện
- I = 0 . B = 0 . H ≠ 0
Với
Định luật Điện từ trường
sửaCác Định luật điện từ được phát triển bởi nhiều nhà khoa học gia
Định luật Gauss
sửaMật độ điện trường và từ trường trong một diện tích
Định luật Ampere
sửaTừ cảm của cuộn từ dẩn điện
Định luật Lentz
sửaTừ cảm ứng của cuộn từ dẩn điện
Định luật Faraday
sửaĐiện từ cảm ứng của cuộn từ dẩn điện
Định luật Maxwell
sửaTừ nhiểm của cuộn từ dẩn điện
Dòng điện
Phương trình điện từ
sửaPhương trình điện từ nhiểm Maxwell
sửaTên Dạng phương trình vi phân Dạng tích phân Định luật Gauss: Đinh luật Gauss cho từ trường
(sự không tồn tại của từ tích):Định luật Faraday cho từ trường: Định luật Ampere
(với sự bổ sung của Maxwell):
Phương trình Sóng điện từ Laplace
sửaĐiện tích
sửaĐiện tích đại diện cho các phần tử mang điện tồn tại trong tự nhiên thí dụ như điện tử âm, điện tử dương, điện tử trng hòa trong nguyên tử điện . Điện tích được hiểu là "vật tích điện". Thí nghiệm cho thấy, mọi vật trung hòa về điện khi cho hay nhận điện tử âm sẽ trở thành điện tích.
Loại Điện tích
sửaCó 2 loại Điện tích là Điện tích âm và Điện tích dương . Điện tích âm tạo ra từ vật trung hòa về điện nhận Điện tử âm . Điện tích dương tạo ra từ vật trung hòa về điện cho Điện tử âm như ở dưới đây
Điện tích Ký hiệu Tích điện Điện lượng Điện trường Từ trường ' Điện tích âm (-) Vật + e Q B Điện tích dương (+) Vật − e
Tính chất Điện tích
sửaMọi điện tích đều có các tính chất sau Điện lượng Q, Điện trường E và Từ trường B được tính theo định luật Gauss ở dưới đây
Điện lượng
sửaĐiện lượng cho biết số lượng điện của Điện tích.
Điện lượng có ký hiệu Q .
- Điện tích âm có ký hiệu -Q . Điện tích dương có ký hiệu +Q
Điện lượng đo bằng đơn vị Coulomb (C) . Đơn vị Coulomb được định nghĩa như sau
- electron.
Điện lượng được tính bằng công thức
Điện trường
sửaĐiện trường cho biết trường điện của các đường lực điện trong một diện tích .
Điện trường có ký hiệu E đo bằng đơn vị V/m
Điện tích âm có các đường lực điện hướng vô . Điện tích dương có các đường lực điện hướng ra .
Điện trường tính bằng công thức
Từ trường
sửaTừ trường cho biết trường từ của các đường lực từ trong một diện tích .
Từ trường có ký hiệu B . Trong hệ SI, B có đơn vị tesla (T) và tương ứng ΦB (từ thông) có đơn vị weber (Wb) do vậy mật độ thông lượng 1 Wb/m² bằng 1 tesla. Đơn vị SI của tesla bằng (newton•giây)/(coulomb•mét).[nb 5] Trong đơn vị Gauss-cgs, B có đơn vị gauss (G) (và 1 T = 10.000 G) Trường H có đơn vị ampere trên mét (A/m) trong hệ SI, và oersted (Oe) trong hệ CGS.[12] và được
Điện tích âm có các vòng tròn lực từ đi thuận chiều kim đồng hồ , Điện tích dương có các vòng tròn lực từ đi nghịch chiều kim đồng hồ.
=Từ trường đượ tính bằng
Định luật tương tác Điện tích
sửaĐịnh luật Coulomb
sửaĐịnh luật tương tác giửa 2 Điện tích .
Định luật Coulomb cho rằng
- Khi có nhiều điện tích nằm kề nhau, điện tích đồng loại sẻ đẩy nhau . Điện tích khác loại sẻ hút nhau . Điện tích âm sẻ hút điện tích dương về hướng mình tạo ra lực hút điện tích còn được gọi là Lực Coulomb
Lực điện tích âm hút điện tích dương về hướng mình được tính bằng định luật Coulomb như sau
Với
- - Lực hút điện tích
- - Điện tích
- - Cách khoảng giửa 2 điện tích
- - Hằng số hấp dẩn điện tích
Từ trên Khoản cách giửa 2 điện tích
Với 2 điện lượng cùng cường độ
Lự Coulomb
Khoảng cách giửa 2 điện tích
Điện trường
Năng lực Điện trường
Năng lươ.ng Điện trường
Định luật Ampere
sửaĐịnh luật tương tác giửa Điện tích và điện
Thí nghiệm cho thây, lực điện tương tác với điện tích làm cho điện tích di chuyển thẳng hàng theo hướng ngang sẻ tạo ra một điện trường . Lực điện tạo ra điện trường được tính theo định luật Ampere như sau
Với
- - Lực điện động
- - Điện lượng
- - Điện trương
Từ trên,
Đường dài di chuyển
Vận tốc di chuyển
Thời gian di chuyển
Định luật Lorentz
sửaĐịnh luật tương tác giửa Điện tích và từ trường .
Thí nghiệm cho thấy, khi điện tích di chuyển qua nam châm, lực từ của nam châm làm cho điện tích di chuyển thẳng hàng theo hướng dọc đi lên hay đi xuống hay theo vòng tròn quỹ đạo đi thuận hay nghịch chiều kim đồng hồ
Định luật Lorentz cho rằng
- Lực từ có phương luôn vuông góc với phương chuyển động của hạt mang điện và làm thay đổi quỹ đạo chuyển động của hạt mang điện. Nếu hạt mang điện chuyển động theo phương vuông góc với đường cảm ứng từ thì hạt sẽ chuyển động theo quỹ đạo tròn, nếu hạt chuyển động theo phương không vuông góc với đường cảm ứng từ thì quỹ đạo của nó sẽ là hình xoắn ốc .
Điện tích di chuyển thẳng hàng theo hướng dọc đi lên hay đi xuống
sửaTrong trường hợp lực từ của nam châm làm cho điện tích di chuyển thẳng hàng theo hướng dọc đi lên hay đi xuống . Lực từ được tính theo định luật Lorentz như sau
Với
- - Lực Lorentz hay Lực từ động
- - Điện lượng
- - Vận tốc
- - Từ cảm
Từ trên,
Vận tốc di chuyển
Đường dài di chuyển
Thời gian di chuyển
Điện tích di chuyển theo vòng tròn quỹ đạo đi thuận hay nghịch chiều kim đồng hồ
sửaChuyểng động cân bằng của 2 lực lực vô vòng tròn và lực từ động
Vận tốc di chuyển
Bán kín vòng tròn
Lực Điện từ
sửaLực điện từ có ký hiệu đo bằng đơn vị Newton N . Lực điện từ tạo ra từ tổng của 2 lực , Lực động điện và Lực động từ được tính bằng công thức sau
Với
- - Lực động điện từ
- - Lực động điện
- - Lực động từ
- - Điện lượng
- - Điện trường
- - Từ trường
- - Vận tốc
Từ trên,
- với
- với
- với
Đường dài điện trường
Đường dài từ trường
Đường dài điện từ trường
Điện từ va dẩn điện
sửaĐiện trường của dẩn điện
sửaTừ trường của dẩn điện
sửaTừ cảm
sửaTheo Định luật Ampere, cường độ Từ cảm trên dẩn điện được tính như sau
- . Với
Nam châm điện Hình Công thức Nam châm điện Từ trường của cộng dây thẳng dẩn điện Nam châm điện Từ trường của vòng tròn dẩn điện Nam châm điện Từ trường của N vòng tròn dẩn điện
Từ nhiểm
sửaPhương trình và Hàm số Sóng điện từ Laplace
sửaTrong môi trường vật chất , H≠0
sửaPhương trình vector dao động điện từ
sửaDao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường, E và Từ trường, B
Phương trình và hàm sóng điện từ
sửaCho một Phương trình sóng điện từ
Nghiệm của Phương trình sóng điện từ trên cho Hàm số sóng điện từ
Trong môi trường chân không , H=0
sửaPhương trình vector dao động điện từ
sửaDao động điện từ được Maxwell biểu diển dưới dạng 4 phương trình vector đạo hàm của 2 trường Điện trường, E và Từ trường, B
Phương trình và hàm sóng điện từ
sửaCho một Phương trình sóng điện từ
Nghiệm của Phương trình sóng điện từ trên cho Hàm số sóng điện từ